Jour 1 – Résolution du quart de singe

Règles du jeu

Le quart de singe est un jeu multijoueur où à tour de rôle, chacun doit ajouter une lettre pour construire un mot. Le premier qui ne peut plus jouer a perdu. Par exemple, à 2 joueurs, si le joueur 1 commence :

  • J-A-Z-Z-Y : joueur 2 ne peut plus continuer, joueur 1 gagne
  • A-R-B-R-E-S : joueur 1 ne peut plus continuer, joueur 2 gagne

Bref, c’est le jeu parfait pour les longs trajets en voiture.

Stratégie gagnante

Dans tout ce qui suit, on se concentre sur la version à 2 joueurs, et on cherche un moyen de gagner à tous les coups, en commençant.

Un principe fondamental : j’ai une stratégie gagnante s’il existe un coup tel que quel que soit le coup adverse, il existe un coup tel que quel que soit le coup adverse, (etc.) je gagne.

Et ce principe marche sur tous les jeux à 2 joueurs. Rappelez-vous le jeu des allumettes de Fort Boyard, où chaque joueur peut retirer entre 1 et 3 allumettes, et celui qui retire la dernière perd. Si vous lui en laissez 5, vous avez une stratégie gagnante (en d’autres termes, il est foutu) car s’il en retire 1, vous en retirez 3 ; s’il en retire 2, vous en retirez 2 ; s’il en retire 3, vous en retirez 1 ; bref, quel que soit son coup, il existe un coup pour vous qui le force à retirer la dernière allumette.

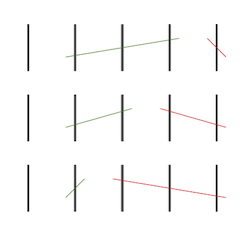
_static/boyard.png

On peut s’intéresser à déterminer algorithmiquement une stratégie gagnante pour le quart de singe. Supposons que notre vocabulaire soit constitué exclusivement des mots {ARBRE, ARBRES, BOB, BOUM, BIS} (assez réducteur, je vous l’accorde). L’ensemble des parties possibles peut être représenté selon l’arbre suivant (à lire de haut en bas). Les sommets où l’on perd sont colorés en rouge, les sommets où l’on gagne sont colorés en vert.

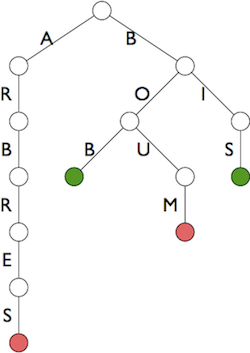
_static/qds.png

Commencer par A nous conduirait à notre perte (A-R-B-R-E-S : l’adversaire gagne). En revanche, si on commence par B et que l’adversaire dit O, si on dit U, BOUM perdu. Il faut dire B (BOB) pour gagner.

Ainsi, il suffit de retenir le sous-vocabulaire {BOB, BIS} dans une antisèche pour être sûr de gagner à tous les coups. Je commence par dire B. Si l’adversaire dit O, je dis B et gagne. Si l’adversaire dit I, je dis S et gagne. Dans notre vocabulaire d’exemple, l’adversaire n’a pas d’autre issue. Dès le début, je sais que je vais faire un mat en 3 coups.

Résolution en Python

Voici un programme Python qui détermine la plus petite antisèche (le plus petit sous-arbre gagnant) pour un vocabulaire donné en entrée. Vous pouvez vous amuser à changer la liste de mots, en veillant à respecter la syntaxe (que des caractères alphabétiques, entourés d’apostrophes, séparés par des virgules), sinon Python vous insultera et vous pourrez recharger la page.


(quartdesinge)

S’il y a une chose à retenir de ce code, ce sont ces 4 lignes :

if is_mine:
    node.winning = any(child.winning for child in node.children.values())
else:
    node.winning = all(child.winning for child in node.children.values())

C’est la version Python de la notion de stratégie gagnante définie au-dessus : à un moment où c’est à moi de jouer, je gagne à coup sûr si l’un (any) de mes coups possibles me permet de gagner à coup sûr. À un moment où c’est à l’adversaire de jouer, je gagne à coup sûr si tous (all) ses coups possibles me permettent de gagner à coup sûr.

Ce programme, lancé sur la liste des 386 264 mots de la langue française, nous permet de déterminer une antisèche pour le jeu original : si je retiens seulement {JAZZY, JEANS, JIGGERS, JOJOS, JUKEBOX} (tous sont bien des mots de la langue française), je suis sûr de gagner au quart de singe. (Par exemple, après J-A-Z, l’adversaire est obligé de dire Z, et on gagne en disant Y.)

À vous de jouer

Challenge 1. Si c’est moi qui commence, quelles sont les lettres de l’alphabet à partir desquelles je suis sûr de gagner ?

Challenge 2. Si c’est le joueur adverse qui commence et qu’il choisit une lettre qui ne lui permet pas de gagner à coup sûr, déterminer une antisèche qui me permet de gagner.

Ressources utiles