Jour 3 – Exploration des rues de Paris¶

Énoncé¶

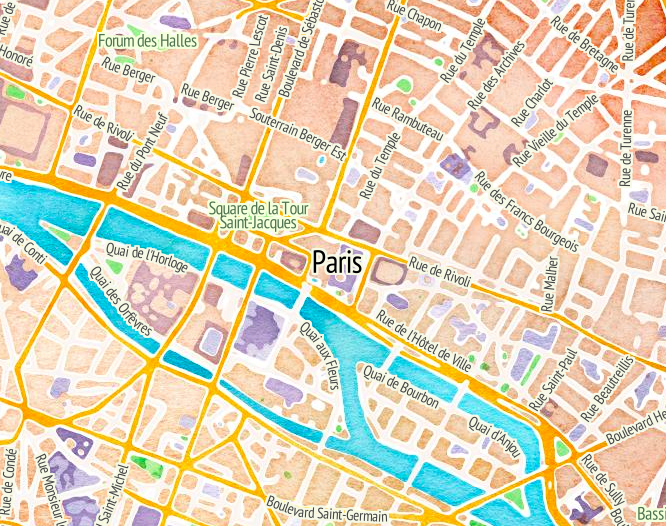
Pour ce faire, le graphe de Paris nous était donné, sous cette forme :

8399 8401 1 4 36
7851 3775 1 10 120
11105 3149 2 6 90
2587 10583 1 26 265
2803 2804 2 7 108

Par exemple, la première ligne signifie : « Il y a une route du coin de rue n° 8399 au coin de rue n° 8401, elle est à sens unique (1), prend 4 secondes et fait 36 mètres de long. » On avait aussi les coordonnées satellite de chaque nœud, mais on ne s’en est pas tous servis.

Et on devait soumettre un fichier texte contenant le trajet pour chacune des 8 voitures. À chaque soumission, on obtenait un score, la distance totale parcourue et – très important – on pouvait visualiser le trajet en couleurs sur la carte de Paris !

Premiers algorithmes¶

Notre algorithme pour une voiture était : choisir à chaque étape la route non déjà visitée de longueur maximale si elle existe, et sinon aller à la plus proche rue non encore visitée (en termes de temps). On a fait 5e, avec 1904 km parcourus (sur 1967 km de rues en tout).

L’algorithme d’une autre équipe : choisir à chaque étape la route non déjà visitée de rapport longueur / durée de parcours maximal si elle existe, et sinon aller à la plus proche rue non encore visitée (en termes de temps). Ils ont fait 2e, avec 1916 km (les premiers étaient à 1923 km). Est-ce que ça veut dire qu’ils avaient un meilleur algorithme ? Pour le critère considéré (la plus longue distance parcourue), on peut seulement dire qu’il s’agissait d’un meilleur algorithme sur l’instance du graphe de Paris (certainement pas sur tous les graphes). (Je rage, mais je suis purement factuel, donc vous ne pouvez pas me contredire.)

Bref, au début on réfléchissait à une manière efficace et élégante de résoudre ce problème. Mais vers la fin de l’épreuve, les gens commençaient à tester n’importe quoi (par exemple, un algorithme qui ne faisait qu’aller à droite pendant 5 heures, et qui était quand même meilleur que 90 % des participants) et au bout d’un moment, ça ressemblait à changer des chiffres au hasard (ou une addition en une multiplication), faire tourner l’algorithme, espérer que le nombre à l’arrivée soit plus grand score. Une vraie loterie.

Et pendant l’épreuve, un gars de notre équipe a une idée. Eulérianiser le graphe. Clairement, on n’avait pas le temps de l’implémenter, mais ça semblait une bonne idée.

Chemin eulérien¶

Vous avez sans doute déjà entendu parler de la maison qu’on peut dessiner « sans lever le crayon ». Un tel graphe, pour lequel il existe un chemin passant exactement une fois par chaque arête, est dit eulérien. En fait on peut montrer qu’un graphe est eulérien si et seulement si pour chaque nœud (intersection), le nombre de flèches entrantes est égal au nombre de flèches sortantes. De plus, il existe un algorithme très simple pour vérifier ça (je l’ai codé sur un smartphone pour un DM d’agrég’) :

def cycle_eulerien(graphe, depart): # Algorithme de BB (je donnerai son nom complet s'il est d'accord)
    dejavu = set()
    chemin = []
    def parcours(v, profondeur=0): # On parcourt chaque arête au plus une fois => complexité O(|E|)
        for w in graphe[v]:
            if (v, w) not in dejavu:
                dejavu.add((v, w))
                dejavu.add((w, v))
                parcours(w, profondeur + 1)
        chemin.append(v)
    parcours(depart)
    return chemin

Mais le graphe de Paris n’est pas eulérien (faut pas déconner). Du coup il faudrait déterminer quels sommets ont un excédent en flèches entrantes, quels sommets ont un excédent en flèches sortantes, et les raccrocher via des plus courts chemins. La terminologie académique étant : faire un couplage de poids minimal entre sommets.

Couverture complète¶

Après le concours, Google a laissé le système de soumission en ligne et donc 2 jours après, une équipe d’Ulm a implémenté l’algorithme consistant à eulérianiser le graphe de Paris. Ils ont donc réussi à obtenir le score maximal de 1967 km. C’est d’autant plus drôle que la limite de 5 heures fixée par Google (18000 secondes) avait été déterminée de la manière suivante : Google avait fait tourner ses algorithmes d’optimisation de manière à leur faire parcourir tout Paris ; ils avaient calculé le temps obtenu et avaient retiré 20 % pour le concours.

Moralité, Ulm : 1 – Google : 0.

À demain !